Pasteur Labs recently ran a hackathon for a group of students at the intersection of scientific computing and machine learning. Since we only had three days, we decided to stick to the basics and cover some textbook SciML applications. Just kidding! We posed an ambitious optimization task: Using differentiable physics programming, maximize the energy produced by a nuclear fusion device across an entire "shot" with respect to a high-dimensional parameter space. Did our participants rise to the challenge? Of course they did.

Our choice of a nuclear fusion application was deliberate. At Pasteur, our mission is to build Nobel-Turing technologies for the advancement of science and society for all humankind. "Nobel" refers to making Nobel-caliber scientific discoveries. "Turing" means arriving at those discoveries through highly autonomous techniques and workflows. One of the bets we're making in this direction is in nuclear fusion. Fusion energy is one of the grand challenge of 21st century science: to bottle a star here on Earth, and unlock an energy source with limitless clean fuel, would fundamentally transform the energy landscape. Our conviction is that Simulation Intelligence has a big role to play in making fusion energy a reality.

Z-Pinch fusion

One of the many promising fusion approaches currently being pursued around the world is Zap Energy's Sheared Flow-Stabilized Z-Pinch¹. A Z-Pinch uses the ubiquitous "pinch effect" of plasmas---the same physical force that causes parallel current-carrying wires to swing together---to compress a column of plasma. As the current through the device ramps up, this compression continues until the plasma is hot and dense enough to undergo nuclear fusion.

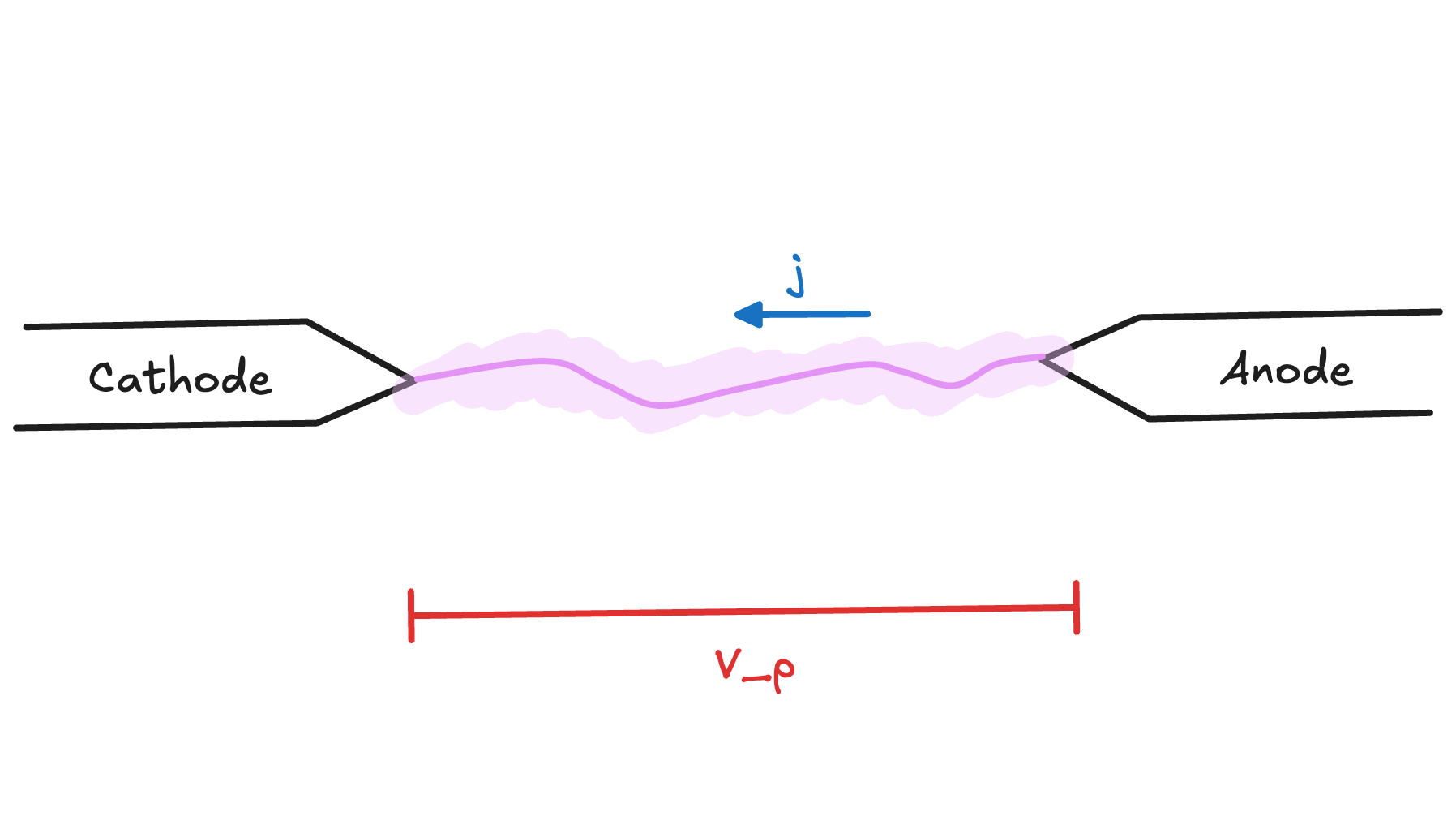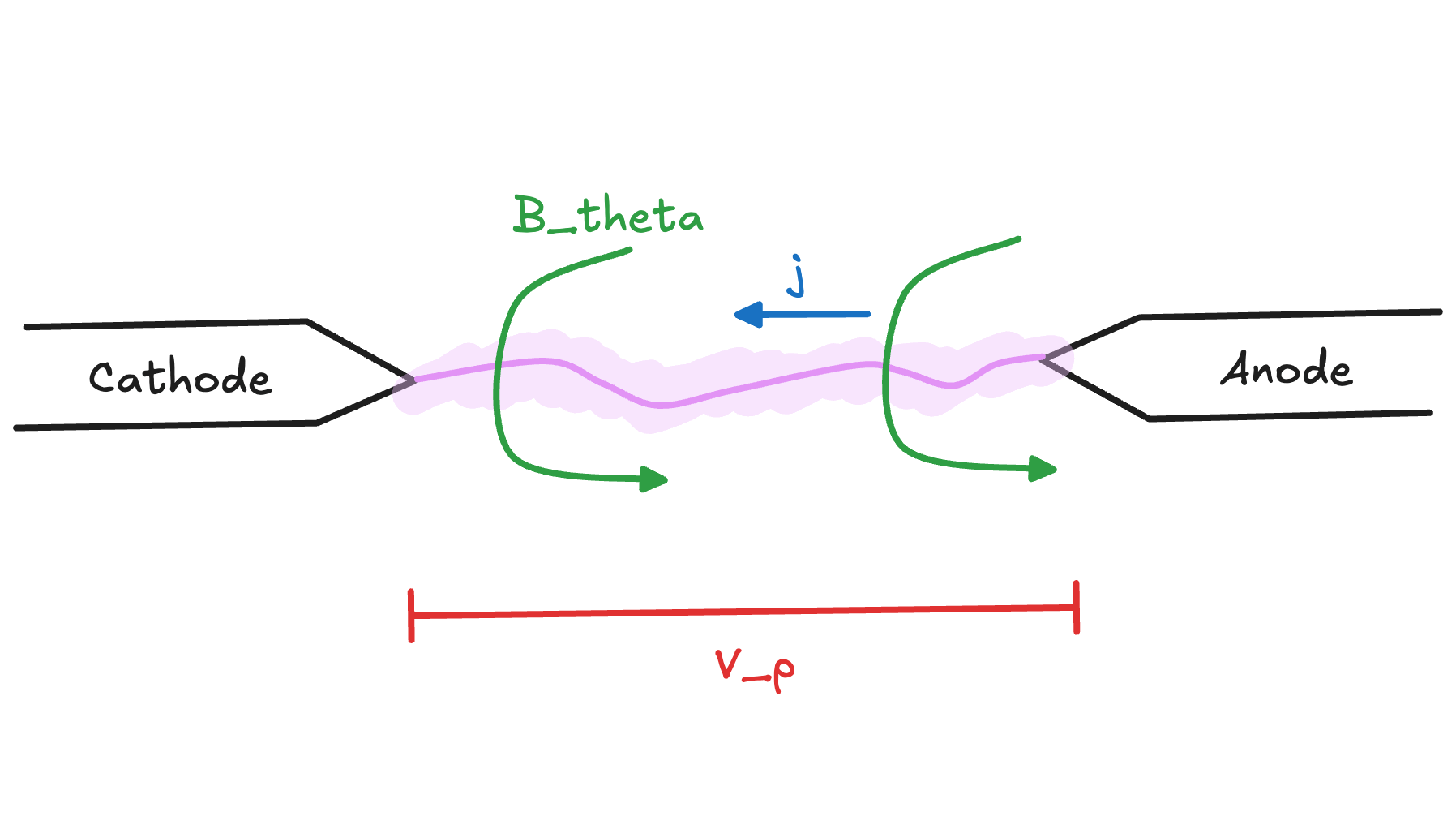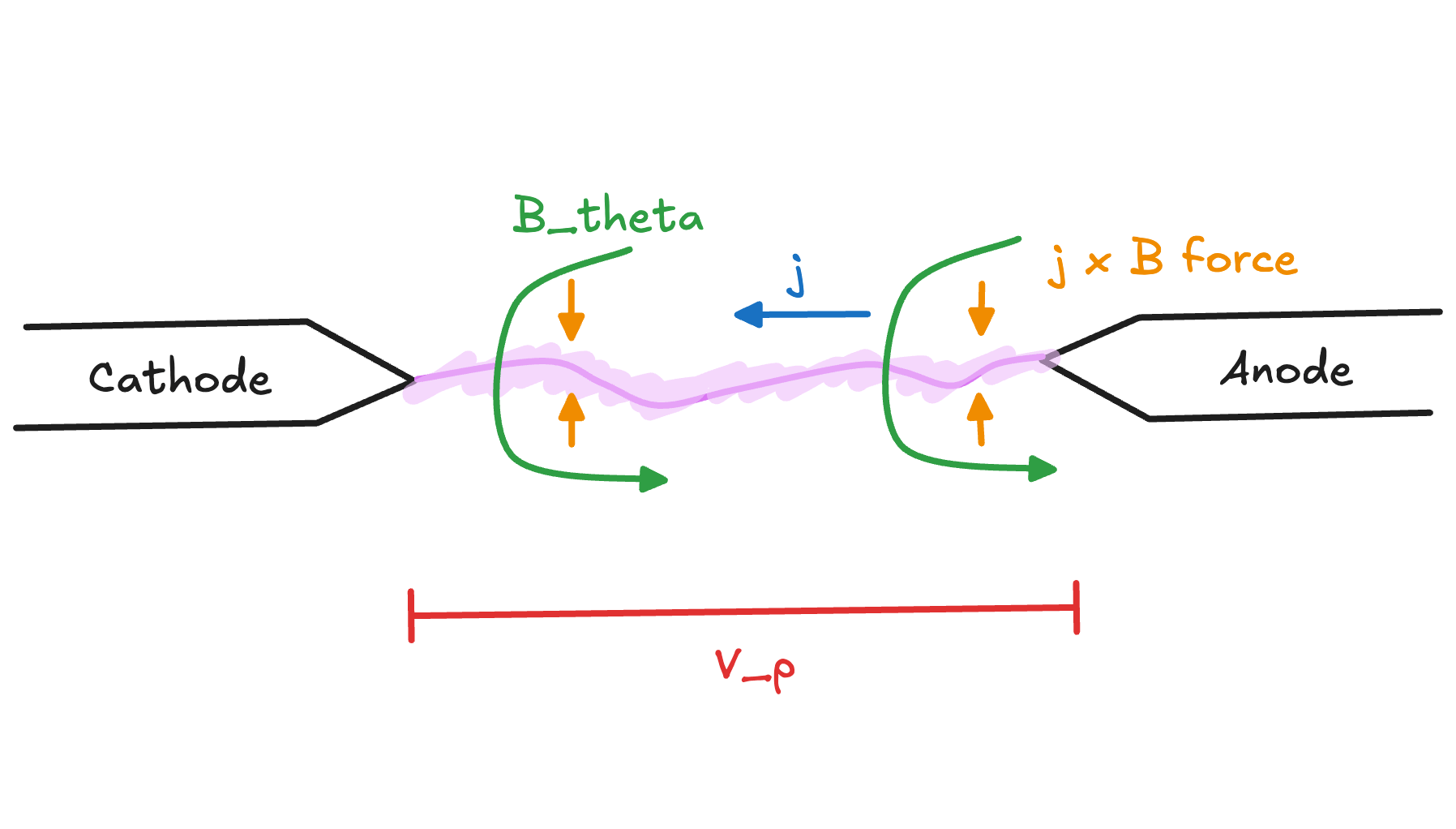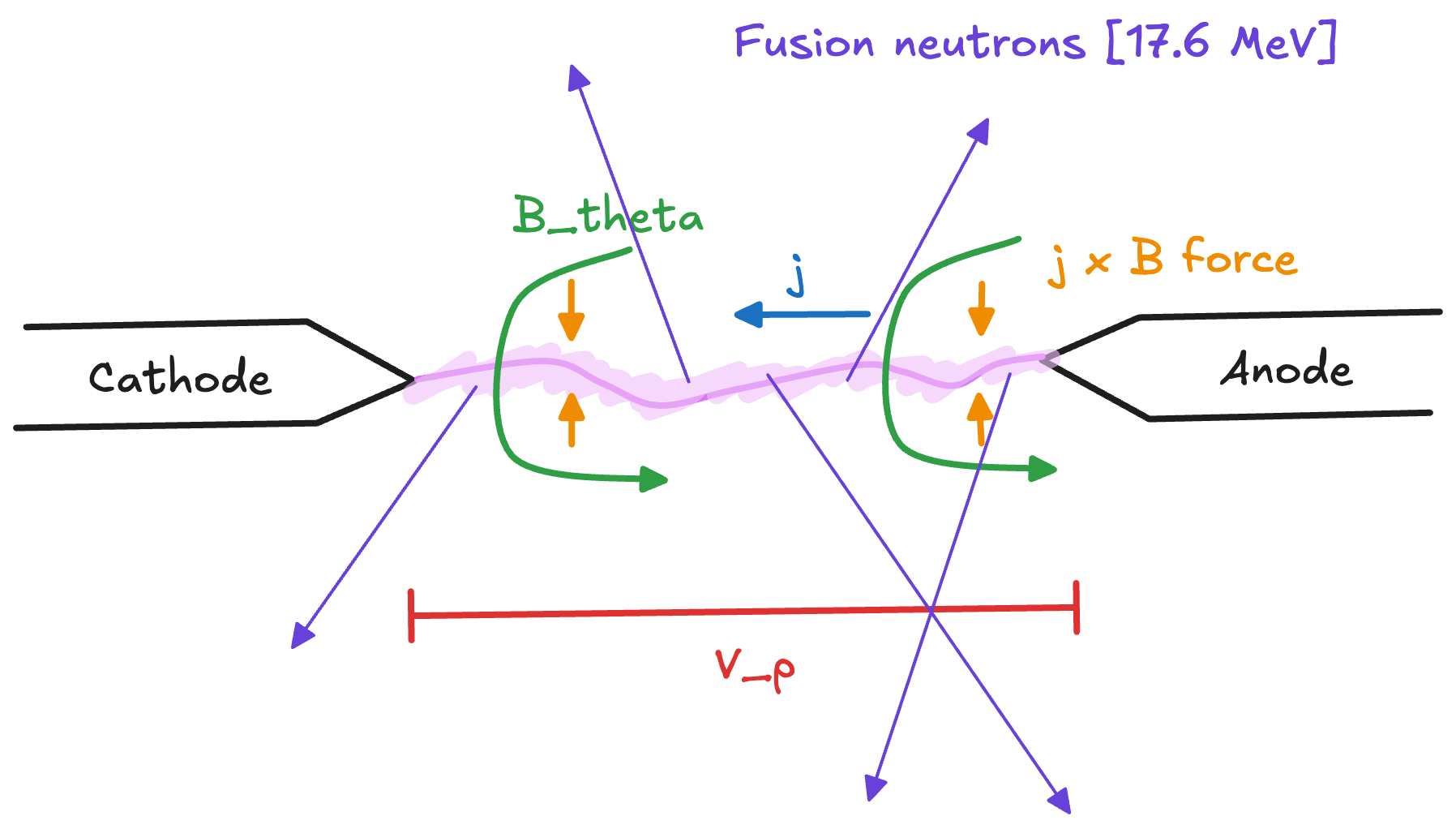
A discharging Z-Pinch is essentially one big electrical circuit. The device is prepared by charging its capacitor banks to many kilovolts. To fire a "shot", operators close a switch and the capacitors discharge their energy through a plasma that forms and compresses within microseconds. The plasma in a Z-Pinch is also a circuit component. Fusion performance depends critically on how this plasma circuit component behaves. To understand the whole device, we need to combine mathematical models from two different domains: electrical engineering and plasma physics.

The output of such a whole device model is a shot trajectory: the time-dependent history of the plasma and circuit state. To understand a shot's performance in terms of fusion, the best point of view is a density-temperature plot:

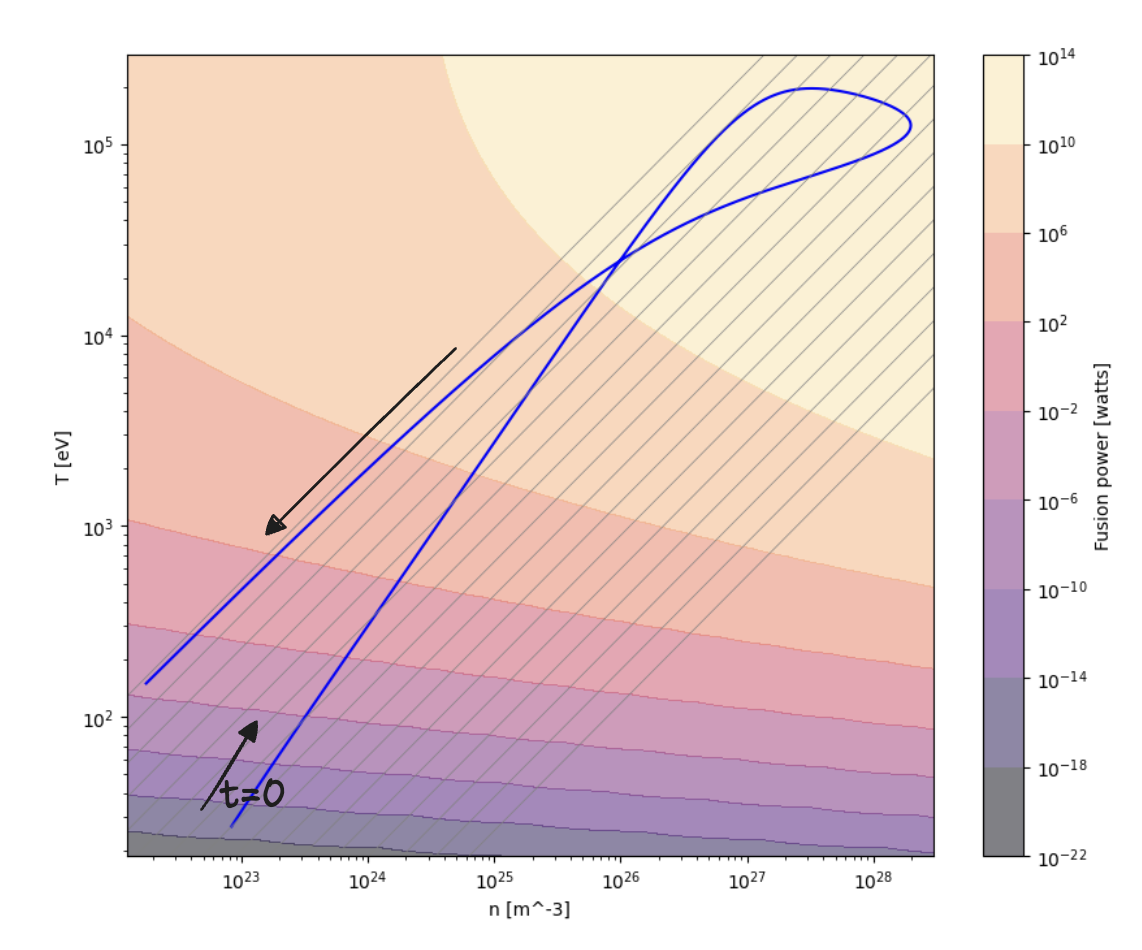
Fig. 1 encapsulates the dynamics of a single shot as it compresses and heats up from its initial state to fusion-relevant conditions. The longer our trajectory stays in the top-right of this plot, the higher the total fusion energy produced. This trajectory depends on numerous variables: the details of the circuit driving the Z-Pinch, the geometry of the plasma region, and the initial conditions of the plasma before compression.

Optimizing a Z-Pinch device combines multi-physics modeling with a complex, high-dimensional loss landscape. In other words, a perfect problem for differentiable physics programming. Our hackathon project tackled each of these two aspects in turn:

1. Complete the implementation of a Z-Pinch whole device model, combining the circuit equations with a plasma model, in a differentiable programming framework.
2. Use the differentiable whole device model to pose and solve an optimization problem for fusion yield.

In the next section, we'll dive into the differentiable whole-device model in more detail and highlight how Tesseracts helped us iterate quickly. Then we'll share some of the results obtained by the hackathon participants.

The differentiable physics programming approach to Z-Pinch modeling

The RLC circuit model

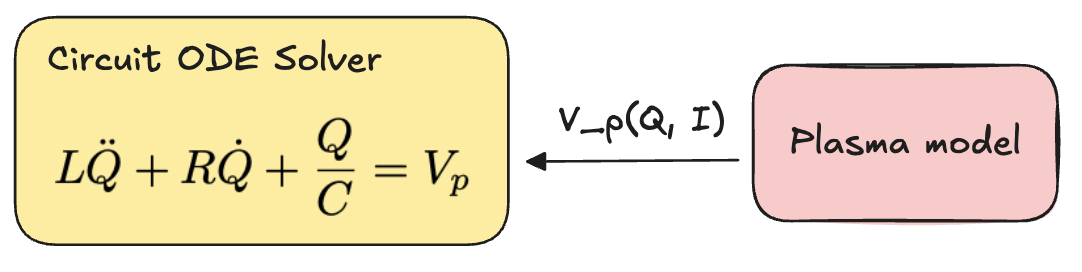
The Z-Pinch is powered by a capacitor bank, charged to multiple kilovolts. When a switch is flipped to fire the shot, the capacitors discharge in a matter of microseconds. To model the dynamics of this fast discharge, hackathon participants used the equation for a series RLC circuit:

Here, $Q$ represents the charge remaining in the capacitor, $C$ is the capacitance, $L$ is the circuit inductance, and $R$ the resistance. On the right-hand side we have $V_p$, the voltage across the plasma. The goal is to solve this second-order ordinary differential equation for $Q(t)$. We are given the circuit parameters $R, L,$ and $C$. It remains to find an expression for $V_p(Q, I)$, where $I = \mathrm{d}Q/\mathrm{d}t$ is the current through the circuit in amperes. The voltage $V_p$ is a function of the plasma state: the lower the electrical resistance of the plasma, the smaller the voltage required to drive a given current through it. To solve this problem, we require a mathematical model of the plasma between the Z-Pinch electrodes:

Leveraging the power of JAX

Unfortunately, rather than giving us the mapping $I \mapsto V_p$, the plasma models available to us give the reverse mapping: $V_p \mapsto I$. It is easy to apply a voltage $V_p$ as a boundary condition, but this voltage is precisely the quantity that we're trying to find! We need to formulate the circuit-plasma coupling as an inverse problem:

What voltage $V_p$, when applied across the plasma, results in a given current $I$?

To solve this inverse problem, we use---you guessed it---differentiable programming! For now we'll assume that the plasma model, written in JAX, implements an abstract interface:

I = PlasmaModel(V_p)

To invert this relationship and solve for $V_p$, we can use the Newton-Raphson method, using jax.grad to obtain the gradient $dI/dV_p$. Including the Newton solve, the component diagram for our whole-device model looks like this:

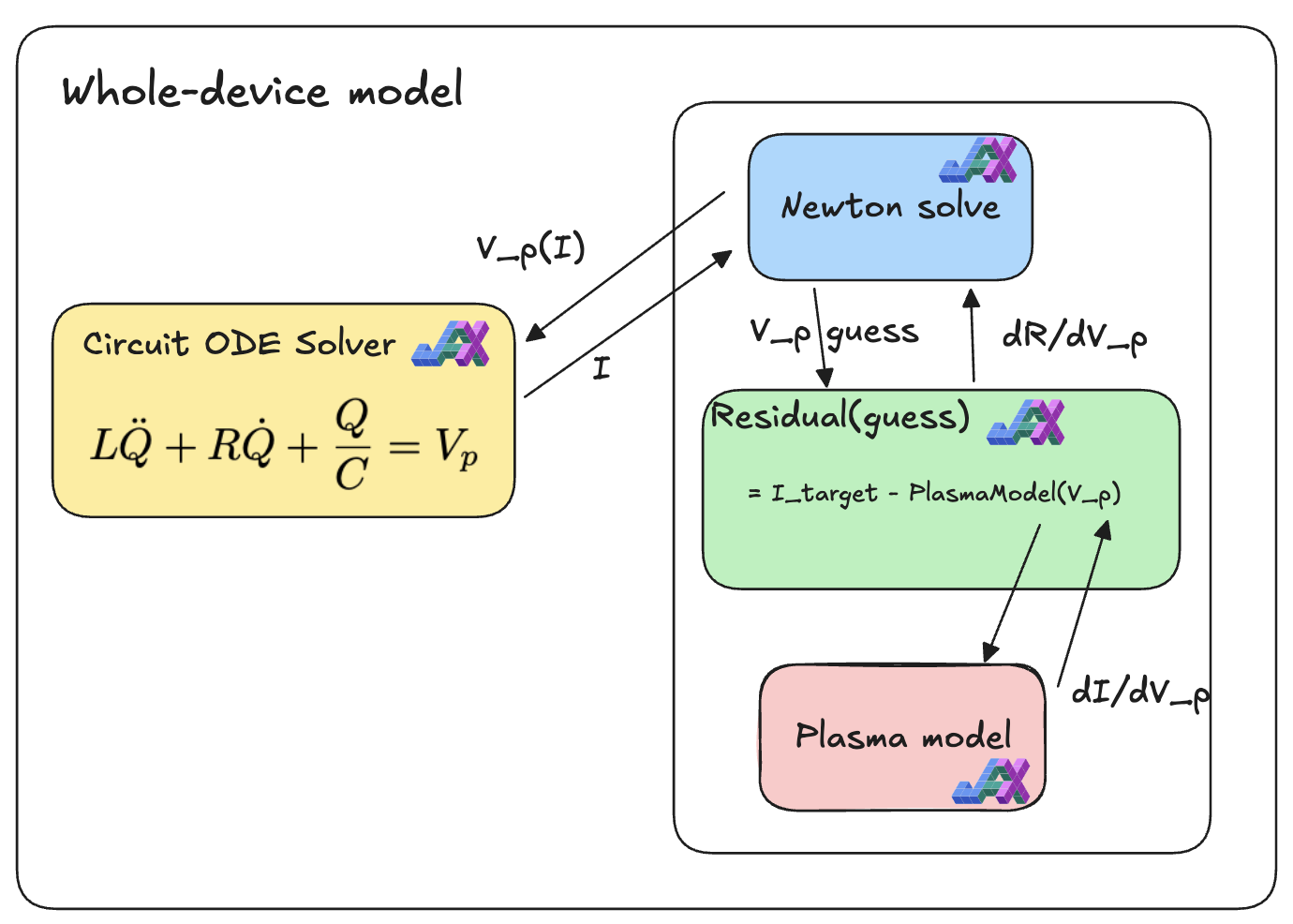
By implementing each component in JAX, we obtain an end-to-end differentiable solver. Similar to NeuralODEs, we can take derivatives of the whole solution trajectory with respect to parameters like $R, L,$ and $C$.

Tesseracts for swappable plasma models

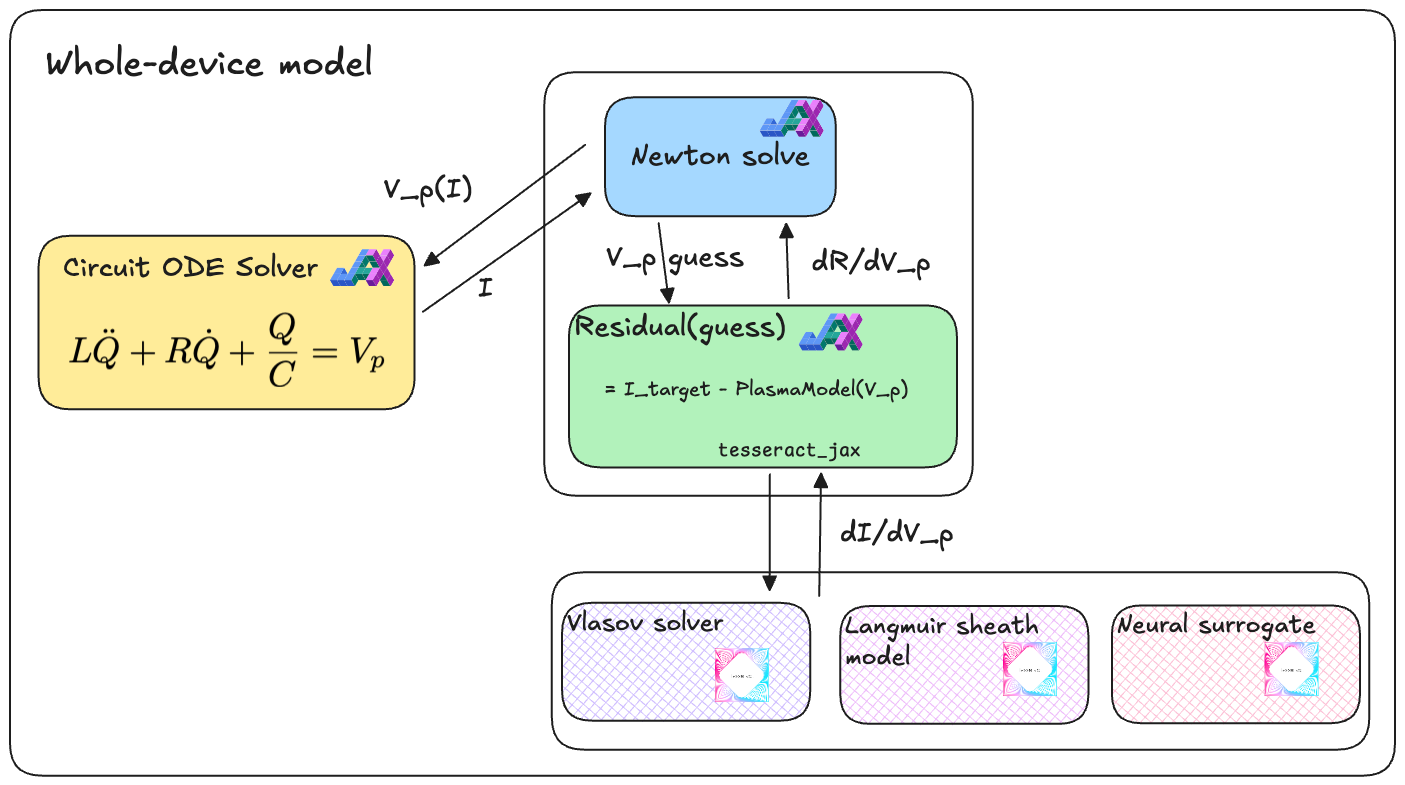
The cardinal rule of computational plasma physics is to choose the simplest mathematical model that will give the right answer. Unfortunately in this case, that model is the notoriously high-dimensional Vlasov-Poisson system of equations. A kinetic model, which explicitly represents the distribution of particle velocities rather than assuming a Maxwellian distribution, is necessary to accurately capture the behavior of the Langmuir sheath that appears at the plasma-electrode boundary.²

With that said, there are simpler approximations to the cross-sheath plasma current that, if not completely accurate, can help build intuition for how the whole-device model behaves. Crucially, such approximations provide us with an approximate answer much, much faster than the steady-state partial differential equation (PDE) solution required for the Vlasov-Poisson system. On the other hand, it may be possible to train a machine learning surrogate model for the PDE solver, which would be both accurate and fast.

To take advantage of the variety of plasma models available to us, we define a plasma model interface. The whole-device model is compatible with any plasma model that implements the proper interface. Our plasma model interface is defined using Tesseracts, a toolkit for autodiff-native software components. Tesseracts allow us to define a schema for the plasma-circuit interaction and implement it with multiple plasma models, each having different accuracy and performance characteristics. Using tesseract-jax, these Tesseracts interoperate seamlessly with JAX, including JIT compilation and automatic differentiation (both forward- and reverse-mode).

Results of the hackathon

The hackathon participants began by implementing the coupled circuit-plasma models using JAX. Successfully implementing the Newton solve in the whole-device model was our first checkpoint, as well as a compelling use-case for differentiable programming. At this point, you have a functioning simulation of a Z-Pinch device, enabled by end-to-end differentiation of a plasma simulation.

Having completed the implementation of the differentiable whole-device model, the students were challenged to formulate and solve an optimization problem for some aspect of the fusion reactor. One group of students chose to optimize with respect to initial voltage across the plasma gap, holding the circuit variables constant. This is related to selecting an optimum "adiabat", or line of constant entropy, to begin the compression. The results are a striking illustration of the power of gradient-based optimization: in just a handful of costly whole-device model solves, the optimizer finds a two-order of magnitude improvement in peak fusion power output:

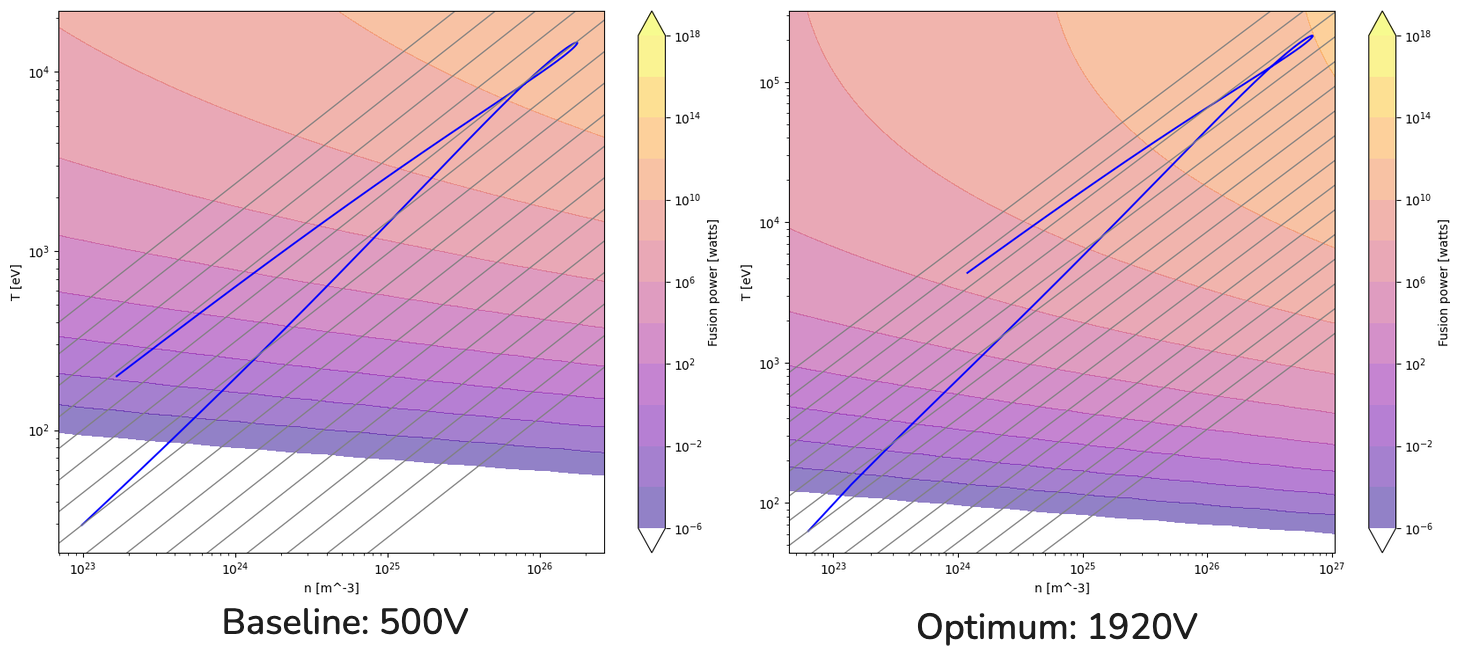
Just as importantly, the gradient-based methodology has no trouble with higher-dimension optimizations: the same group ran a two-parameter optimization with respect to voltage and initial temperature, which demonstrated further improvements over the one-parameter optimization.

Another student, frustrated by the slow runtime of the Vlasov sheath solver, invested time gathering data to train a neural surrogate model: By implementing a basic tesseract_api.py module, he was able to easily slot this neural network, implemented in PyTorch, into the JAX-based whole-device model. Crucially, when he ran the same optimization problem as the first group, his code gave the same result: 1920 volts. To me this was a validation of what we're trying to do here at Pasteur: unlock Simulation Intelligence workflows for science by taking care of the boring parts.

I'm grateful to Jingwei Hu and the other organizers of the Summer School and Hackathon on Structure-Preserving Scientific Computing and Machine Learning for the opportunity to work with such a talented and engaged group of students. Stay tuned for more nuclear fusion-related work coming out of Pasteur Labs!